计算机系统漫游

生成可执行文件的过程

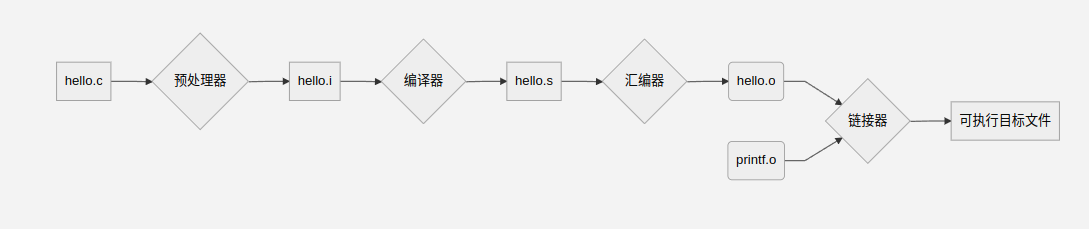
hello.i 文件是在 hello.c 的基础上进行了宏替换，头文件展开等操作。

编译器将C代码转变为汇编语言程序，而汇编器将汇编语言程序转变为机器语言，而不是汇编器将C代码转变为汇编语言。

汇编语言为不同的高级语言提供了相同的输出语言。任何高级语言都需要先转为汇编语言，因为汇编语言才是和机器语言一一对应的。 汇编语言的种类取决于电脑使用的 CPU 指令架构。所以机器代码和汇编代码的移植性比高级语言差许多。

printf 函数在单独预编译好的 printf.o 的文件中，这个文件需要以某种方式合并到 hello.c 文件中，链接器就负责此过程。

系统的硬件组成

总线

总线在各个部件中传输信息字节。总线被设计成传送定长的字节块，即 字（word） ，目前大多数计算机要么是4个字节（32位），要么8字节（63位）。由于每次只能传送定长的字节块，所以C语言中的整型提升意义就在于此。
I/O设备

最基本的I/O设备：键盘，鼠标，显示器，磁盘。
主存

主存又一组 动态随机存取储存（DRAM） 芯片组成。
处理器
处理器看上去是指令集架构的简单实现，大多数离不开下面几个操作：
- 加载：从主存复制数据到寄存器。
- 存储：从寄存器复制数据到主存。
- 操作：把两个寄存器的内容复制到ALU（算术/逻辑单元），ALU对其进行算术运算，并将结果放在一个寄存器中保存结果。
- 跳转：指向下一条指令。

高速缓存

运行程序时，需要先将磁盘中的代码复制到主存中，再由主存复制到 CPU 并运行程序，这些复制便是额外开销，减慢了程序真正工作的效率。

所以目前已经有了 CPU 和内存结合的技术，以解决数据运输的巨大开销。

当下，存取速度远慢于 CPU 计算速度，未来想要进一步提高计算机运行速度，存取技术才是突破口。

为了缓解这样巨大的复制和运输开销，高速缓存储存器 应运而生。

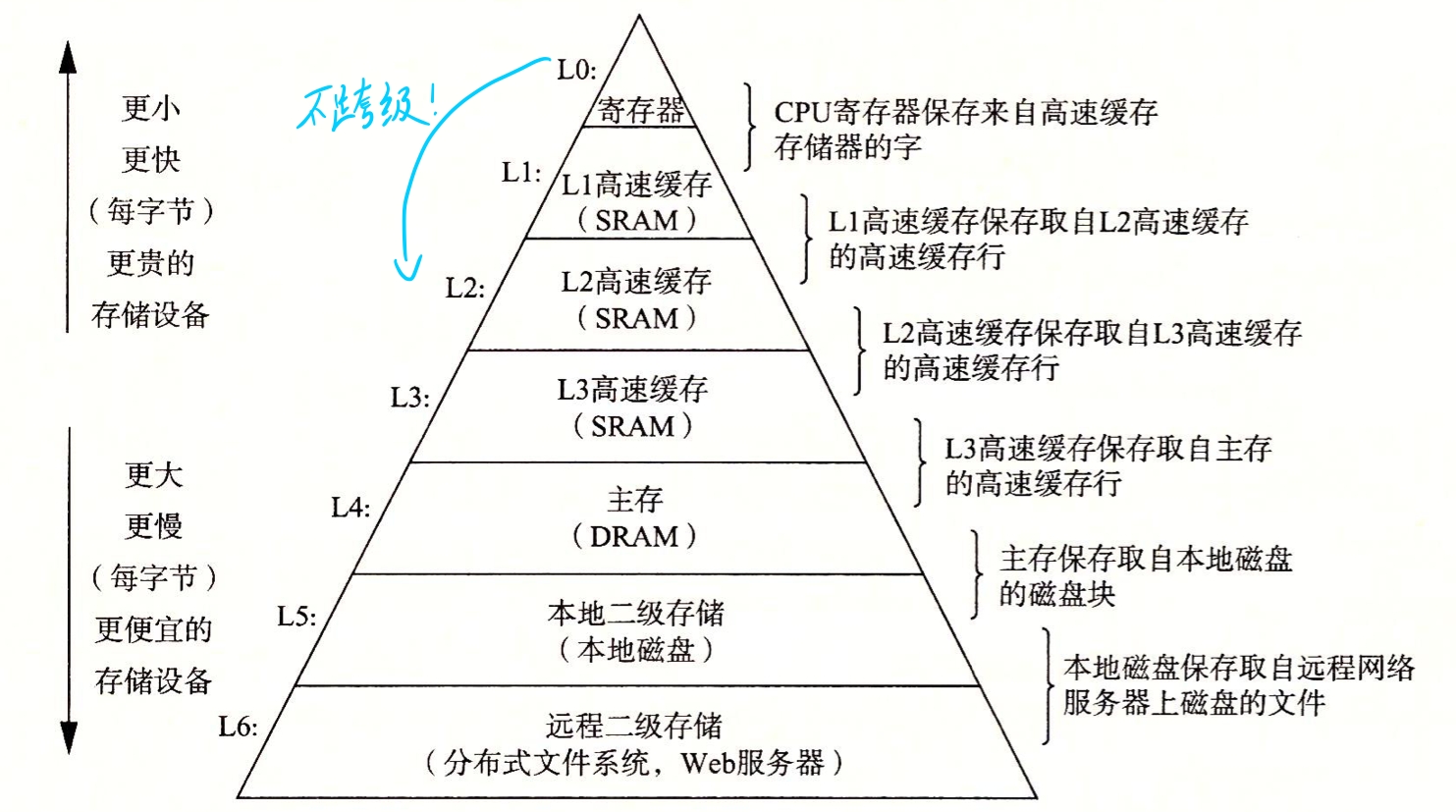
L1，L2，L3高速缓存由 静态随机访问储存器（SRAM） 实现。

储存器的层次结构的主要思想：上一级储存器作为低一层存储器的高速缓存。

操作系统管理硬件

操作系统是应用程序和硬件直接的一层软件，所有应用对硬件的操作都必须通过操作系统来进行，即系统调用。

操作系统的两大功能：

防止硬件被失控的应用滥用。
向应用程序提供简单一致的机制来控制复杂而大不相同的低级硬件设备。

简单而言，操作系统给应用提供硬件的一种抽象。

操作系统通过几个基本的抽象概念（进程，虚拟内存，文件）来实现这两个功能：

文件是对 I/O 设备的抽象。
虚拟内存是对主存和磁盘 I/O 设备的抽象。
进程是对处理器，主存和 I/O 设备的抽象。

进程

进程是操作系统对一个正在运行的程序的一种抽象。 一个 CPU 看上去像是在并发地执行多个进程，这是通过处理器在进程间来回切换实现的。操作系统实现这种交错执行的机制称作 上下文切换 。操作系统保持跟踪进程运行所需的所有状态信息，这种状态也就是上下文，包含许多信息，如：PC和寄存器的值，主存的内容等。任何时刻，单处理器只能执行一个进程的代码。 操作系统从当前进程转到其他进程时，就会保存当前的上下文，并恢复新进程的上下文，新进程就会从之前停止的地方开始。

进程间的切换由操作系统内核（kernel）管理。内核不是单独的进程，而是系统管理全部进程所用代码和数据结构的集合。

文件

Linux哲学：一切皆文件

文件就是字节序列，仅此而已。 在 Linux/Unix 中，每个 I/O 设备，包括磁盘，键盘，显示器甚至网络，都可以看作为文件。所有输入输出操作都是由 Unix I/O 的系统函数调用读写文件来实现的。文件向应用程序提供了统一的视角来看待各种 I/O 设备，大大简化了程序员的工作量。

Amdahl定律

想要显著加速整个系统，必须要提升全系统中相当大部分的速度 。

如果系统中 60% 的部分加速到无需时间，那么整个系统最终的加速比也只有 2.5X

信息的处理和表示

信息 = 位 + 解释

由于不同数据类型有不同的底层实现原理，导致它们的行为也大不相同，比如整形能够进行结合律和交换律，而浮点数却不行。整形是精确的，而浮点是近似的。对相同的位进行不同的解释，得到的结果也大不相同。

信息存储

字节（byte）是最小的可寻址单位（操作单位），而不是内存中单独的位。 每个字节由唯一的数字表示，表示其地址，所有字节的地址集合构成了 虚拟地址空间 。程序数据，指令和控制信息完全在虚拟内存空间中管理。

C编译器将指针和类型信息联系起来，如此便可以根据指针值的类型来生成不同的机器级代码。

实际上，机器代码中并不包含关于数据类型的信息 。问题：那么运行时，CPU 怎么知道用什么方式来解释位？

十六进制

一个十六进制数 = 4个位 ，两个十六进制数 = 2个位 = 1个字节

比如：0x173A4

字数据大小

字长（word size）指明了指针的大小，决定了虚拟地址空间的最大大小 。

64 位机器大多可以运行 32 位程序，而 32 位机器无法运行 64 位程序。”32位程序“ 或 “64位程序” 区别在于该程序是如何编译的，而不是其运行的机器类型。

同时，C数据类型的大小也受字数据大小的影响。

char 常用于储存单个字符，但它也可以用来储存整数值，因为其本质仍是整数。然而并不值得这样做，编译器有可能生成额外代码将 char 变为 int，造成不必要的开销。

为了数据类型大小对机器的依赖，ISO C99 引入了大小固定的数据类型，如：int32_t，int64_t 。

C标准仅规定 char 的大小必须为 1 字节，其他类型仅规定了下限，而没有规定上限。

大部分数据类型都默认编码为有符号类型，但 char 是个例外，C标准不保证这一点，尽管大多编译器视其为有符号数。

寻址和字节顺序

小端（little endian）： 高位在高地址（违背直觉）

大端（big endian）： 高位在低地址（符合直觉）

如表示：0x01234567

一旦选定了特定操作系统，字节顺序也就确定了。

如何确定大小端？

int a = 0x12345678;
	char *b = (char*)&a;
	if (*b == 0x78)
		cout << "little endian" << endl;
	else
		cout << "big endian" << endl;

union Demo
	{
		char ch;
		short sh;
	}demo;
 
	demo.sh = 0x0001;//小端：0x0100    大端:0x0001
 
	if(demo.ch == 0x01)
	{
		cout << "little endian" << endl;
	}
	else
	{
		cout << "big endian" << endl;
	}

移位运算

左移 k 位时，丢弃最高的 k 位，并在右边补上 k 个 0 。 右移时，分为 算术右移 和 逻辑右移 ：

算术右移：左端补上 k 个 有效位 的值。

逻辑右移：左端补上 k 个 0

C语言标准没有明确定义有符号数的右移采用哪种方式，但几乎所有编译器和机器都对有符号数采用算术右移。无符号数只能采用逻辑右移。

在许多机器上， 实际的位移量 = k % w （w是数据类型所占位数），比如 int a = 0x12345678 << 36 ，实际上的的位移量应该是 36%32=4 。不过此行为对于C程序而言是未定义的（java特别要求采用上述方式），应保证位移量小于数据所占位数。

补码编码

C/C++ 支持有符号数（默认）和无符号数，java 只支持有符号数。

C语言标准并没有要求有符号数的表示需用补码，但基本上所有实现都采用的补码。相反，Java标准要求必须用补码。

补码编码用于有符号整数，不同于无符号数编码，补码编码将最高有效位解释为负权，如下：

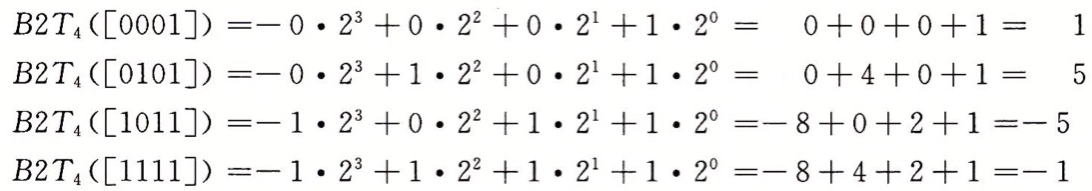
即：当符号位为1时，为负数；符号位为0时，为负数。

补码如此设计是为了让计算机用加法来实现减法，因为计算机只有加法器。而减法的实现正是通过最高位截断来实现的，如下图：

至于原码和反码，只是为了帮助我们快速地计算相反数而引入的概念，个人认为学习时最好不要自动引入这两者，否则很容易混乱。

A - B = A + (-B)，减一个正数B，等于加上B的相反数，即B的补码 。对计算机而言，A 和 B 本来就是采用的补码，所以 B 本来就是负数，不存在 -B 这一说。只是对人而言，当补码为负数时不太好计算，所以引入原码和反码来辅助计算(具体见后文) ，就可以很方便的把减 B 变为加上 B 的相反数。

浮点数中会使用的原码的概念。

补码的属性：

|MIN| = |MAX| + 1

这会造成细微的计算错误： -MIN = MIN

所以：X > Y != (-X) < (-Y)
最大的无符号数比最大的有符号数的两倍还大1。

简单了解一下原码，反码和补码的关系，以应对计算：

真值：带符号位的机器数对应的真正数值称为机器数的真值。

原码：符号位加上真值的 绝对值 , 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:

[+1]原 = 0000 0001

[- 1]原 = 1000 0001
反码：正数的反码是其本身，负数的反码是在其原码的基础上, 符号位不变 ，其余各个位取反。

[+1] = [00000001]原 = [00000001]反

[- 1] = [10000001]原 = [11111110]反
补码：正数的补码就是其本身，负数的补码是在其原码的基础上, 符号位不变 ，其余各位取反, 最后+1. (即在反码的基础上+1)

[+1] = [00000001]原 = [00000001]反 = [00000001]补

[-1 ] = [10000001]原 = [11111110]反 = [11111111]补

一般情况下不要引入这几个概念，极易混。对于整形的储存方式，就只分为无符号编码和补码。

将二进制数（无论补码还是无符号编码）取反加1（补码）的结果和原二进制数相加，其和为0 。

对补码而言：-X = ~X + 1

原码, 反码, 补码详解

有符号数和无符号数的转换

当强制地转换在有符号类型和无符号类型间转换时，结果的位值不变，只改变解释这些位的方式
当隐式地发生转换时，有如下几个规则：
- 整形提升： signed 符号扩展，unsigned 零扩展。
  
  符号扩展：高位补充符号位的值
  
  零扩展：高位补零
  
  这样做可以在保持值不变的情况下将位数少的二进制数（如8位）转为位数多的二进制数（如32位）。
  
  从直观上理解为什么高位补符号位其值不变：
  
  a = 1110 -> 取反加一 -> 0010
  
  b = 11111110 -> 取反加一 -> 00000010
  
  a和b的相反数相同，故 a = b
- 值保护规则： 仅针对无符号数！ 如果 signed int 可以装下扩展前 unsigned 类型的所有值 ，则提升（零扩展）后将其视为 signed int，反之视作 unsigned int 。
- 无符号数和有符号数混合运算时，有符号数会默认转变为无符号数。 此规则发生在前两个规则之后，具体看后文
  
  应极力避免有符号数和无符号数的混合运算，其差错难以发现！

unsigned char a = 1;
signed int b = -1;
if (a < b)
	cout << "aha";
else
    cout<<"dada";   //结果输出dada
//==================================
unsigned int a = 1;
signed int b = -1;
if (a < b)
	cout << "aha";
else
    cout<<"dada";  //结果输出aha

解释：

第一种情况：
1. unsigned char 和 signed int 比较，首先 unsigned char 采用值保护规则，进行提升，由于 signed int 可以装下 unsigned char 的所有值，所以提升后，a 的类型为 signed int
2. a 和 b 都为 signed int ，直接进行比较，a > b，输出 dada
第二种情况：
1. unsigned int 和 signed int 混合运算，后者变为无符号数，-1 变为 INT_MAX
2. 进行比较，b > a ，输出aha

补码转为无符号数：

关系式

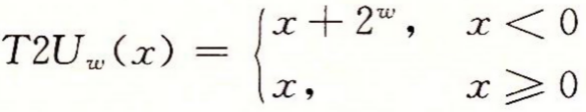
无符号数转换为补码：

关系式

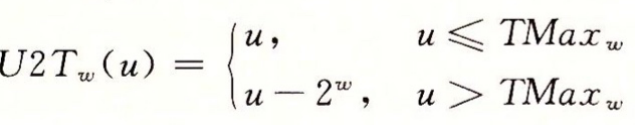
截断

截断无符号数为k位：X’ = X % $2^K$

截断有符号数为k位：X’ = X % $2^K$ ，且最高位作符号位

取模是丢高位，除法是丢低位：

10101 ➗2 = 1110

10101 % $2^4$ = 1110

不论大端还是小段，截断丢弃的都是高位数据！所以下面方法来判断大端还是小端是无效的：

int a = 0x12345678;
char c = a;
if(c==0x78)
    cout<<"little endian"<<endl;

整数运算实际上就是一种模运算形式！

无符号加法

X + Y = ( X + Y ) % $2^k$

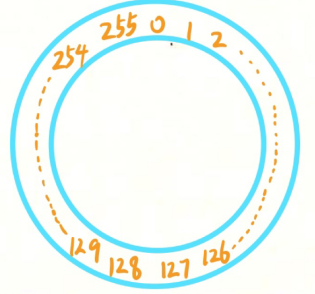
模数加法形成了一种数学结构，即 阿贝尔群 。也就是说，模数加法是 可交换 和 可结合的 。

这说明对于 ( X + Y ) - Y ，无论 ( X + Y ) 是否溢出，始终有 ( X + Y ) - Y = X

这也是整形运算可使用交换律和结合律的原因，而浮点数运算则不可。

补码加法

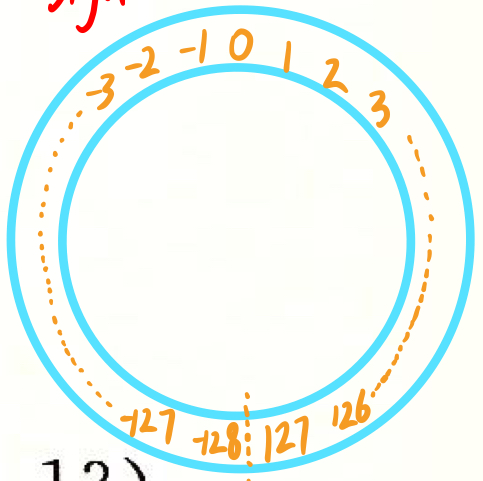
加正数则顺时针，减正数则逆时针。

所以 X<1 不等价于 X-1<0 ，当 X = INT_MIN 时，X - 1 = INT_MAX

此类细节错误经常出现，需要注意！

乘以常数

在大多数机器上，整数乘法往往需要较多的时钟周期，而其他整数运算（加减，位级运算，移位）只需要 1 个时钟周期。因此编译器会试着用移位和加法的组合运算来代替常数的乘法

对无符号和补码值都有： X<< K = X * $2^K$

技巧：考虑一组从位位置 n 到位位置 m （n>m）的连续的 1 ，如对于 14 而言有：

// 0000 0000 0000 1110
//                ⬆⬆⬆⬆
//                3210

则可以有下面两种形式表示此计算：

x << n + x<<(n-1) + … + x<<m
x<<(n + 1) - (x << m)

显然，第二种方法更好。

例如：

X * 14 = X * ( $2^3$ + $2^2$ + $2^1$ ) = (X<<3) + (X<<2)+ (X<<1) = (X<<4) - (X<<1)

3*A = A<<1 + A

除以常数

整数除法比整数乘法需要更多的时钟周期（30乃至更多），所以编译器也会尝试用左移来代替除法。

无符号数和补码数分别使用逻辑右移和算术右移来实现除法。

对于无符号数和补码数，除以 2 的幂的除法 ，都有：X >>k = [X / $2^k$ ]

[ a ] 代表不超过 a 的最大整数，如 [14.5] = 14 ，[-3.5] = -4，即向下舍入。

如果想要变为向上舍入，即令 [ a ] = 超过 a 的最小整数，则需要使用以下 “偏置技术”：

(x+(1<<k)-1)>>1 = [x/ $2^k$ ]

而对于大多数补码机器而言，一般策略是：对正数向下舍入，对负数向上舍入（以0为参考点）。所以一般使用如下方法：

(x < 0?x+(1 << k ) - 1 : x) >> k

这种方法不能推广到任意常数的除法！因为除法没有分配律。

浮点数

在六七十年代，计算机界对浮点数的处理比较混乱，各家厂商都有自己的一套规则，缺少统一的业界标准，这给数据交换、计算机协同工作带来了很大不便。Intel 在研发 8087 浮点数协处理器时，聘请到加州大学伯克利分校的 William Kahan 教授以及他的两个伙伴，来为 8087 协处理器设计浮点数格式，他们的工作完成地如此出色，设计的浮点数格式具有足够的合理性和先进性，被 IEEE 组织采用为浮点数的业界标准，并于 1985 年正式发布，这就是 IEEE 754 标准。IEEE 754完成了对浮点数的统一，所有计算机都支持此标准。

了解浮点数之前，我们先来认识一下 定点数 ：

定点数

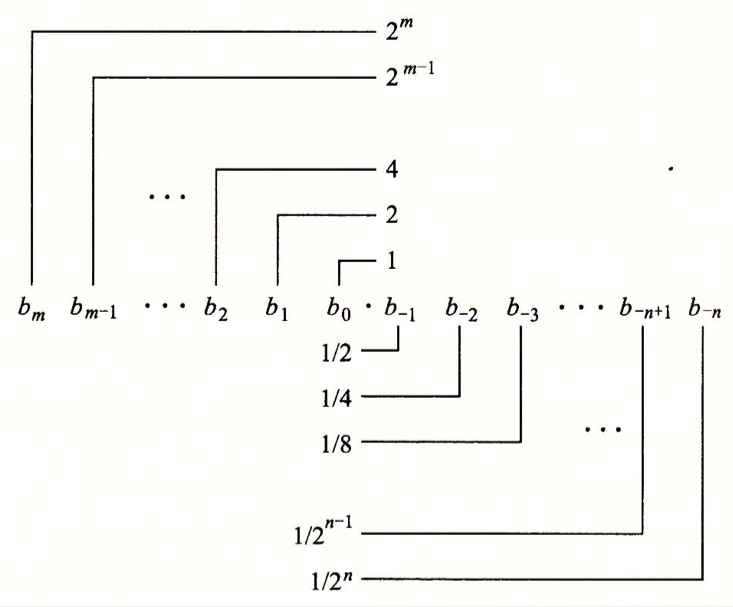
特点

如此一来，小数点就永远在第16位之后，整数部分和小数部分一目了然，不管什么时候，整数部分始终占用16位（不足16位前置补0），小数部分也始终占用16位（不足16位后置补0）。

精度

小数部分的 最后一位可能是精确数字，也可能是近似数字（由四舍五入、向零舍入等不同方式得到）；除此以外，剩余的31位都是精确数字 。从二进制的角度看，这种定点格式的小数，最多有 32 位有效数字，但是能保证的是 31 位；也就是说，整体的精度为 31~32 位 。

范围

将内存中的所有位（Bit）都置为 1，小数的值最大，为 $2^{16}$ - $2^{-16}$ ，极其接近 $2^{16}$ ，换算成十进制为 65536。将内存中最后一位（第32位）置 1，其它位都置0，小数的值最小，为 $2^{-16}$ 。

综述

用定点格式来存储小数，优点是精度高，因为所有的位都用来存储有效数字了，缺点是取值范围太小，不能表示很大或者很小的数字。

浮点数

浮点数使用指数的形式来存储小数，当指数变化时，其小数点的位置也发生变化，故而称之为浮点数。

C语言标准规定 ，小数在内存中以科学计数法的形式来存储，具体形式为：

flt = sign × mantissa × base^exponent

说明：

flt 是要表示的小数。
sign 用来表示 flt 的正负号，它的取值只能是 0 或 1：取值为 0 表示 flt 是正数，取值为 1 表示 flt 是负数。
base 是基数（进制），它的取值大于等于 2。
mantissa 为尾数，或者说精度，是 base 进制的小数，并且 1 ≤ mantissa ＜ base，这意味着，小数点前面只能有一位数字

注意，10.101 × $10^2$ ，10.101 不是尾数，尾数必须要满足 1 ≤ mantissa ＜ base 。
exponent 为指数，是一个整数，可正可负，并且为了直观一般采用十进制表示。

例如：1.0101 × $10^3$ ，其中 1.0101 是尾数，10 是基数，3 是指数。

将小数转换为浮点格式

当 base 取值为 10 时，19.625 的浮点形式为：

19.625 = 1.9625 × $10^1$

当 base 取值为 2 时，将 19.625 转换成二进制为 10011.101，用浮点形式来表示为：

19.625 = 10011.101 = 1.0011101 × $2^4$

19.625 整数部分的二进制形式为：
19 = 1 × $2^4$ + 0 × $2^3$ + 0 × $2^2$ + 1 × $2^1$ + 1 × $2^0$ = 10011
小数部分的二进制形式为：
0.625 = 1 × $2^{-1}$ + 0 × $2^{-2}$ + 1 × $2^{-3}$ = 101
将整数部分和小数部分合并在一起：
19.625 = 10011.101

可以看出，当基数（进制）base 确定以后，指数 exponent 实际上就成了小数点的移动位数 ：

exponent 大于零，mantissa 中的小数点右移 exponent 位即可还原小数的值；
exponent 小于零，mantissa 中的小数点左移 exponent 位即可还原小数的值。

储存

32 位整形（float）： 符号位 1 bit + 指数位 8 bit + 尾数位 23 bit

64 位整形（double）： 符号位 1 bit + 指数位 11 bit + 尾数位 52 bit

符号位： 用 0 表示正数，用 1 表示负数。
尾数位： 当采用二进制形式后，尾数部分的取值范围为 1 ≤ mantissa ＜ 2，这意味着：尾数的整数部分一定为 1（规格化） ，是一个恒定的值，这样就无需在内存中提现出来，可以将其直接截掉，只要把小数点后面的二进制数字放入内存中即可 。对于 1.0011101，就是把 0011101 放入内存。
指数位： 指数必须要有正负，但指数的存储并没有像整形那样采用补码编码的形式，而是采用的是 取中间值 的方式：

在规格化的情况下， float 的指数部分占用 8 Bits，能表示从 0-255 的值，取其中间值 127 （偏置值，bias），指数在写入内存前先加上127，读取时再减去 127 ，正数负数就显而易见了。19.625 转换后的指数为 4，4+127 = 131，131 换算成二进制为 1000 0011，这就是 19.626 的指数部分在 float 中的最终存储形式。

对于 double ，bias = 1023 ，

其中，bias = $2^{k-1} - 1$

根据 exponent 的不同，编码的值可以分为三种情况：

规格化的
非规格化值

非规格化值的尾数不包含隐含的开头的 1，而是 0
无穷大
NaN（Not a Number）

了解规范化数

规格化数的 E = e - bias ，非规格化数的 E = 1 - bias ，其中 E 为实际值，e 为内存值 。非规格化数采用此方式，可以极其巧妙使非规格化值平滑过度到规格化值，如下：

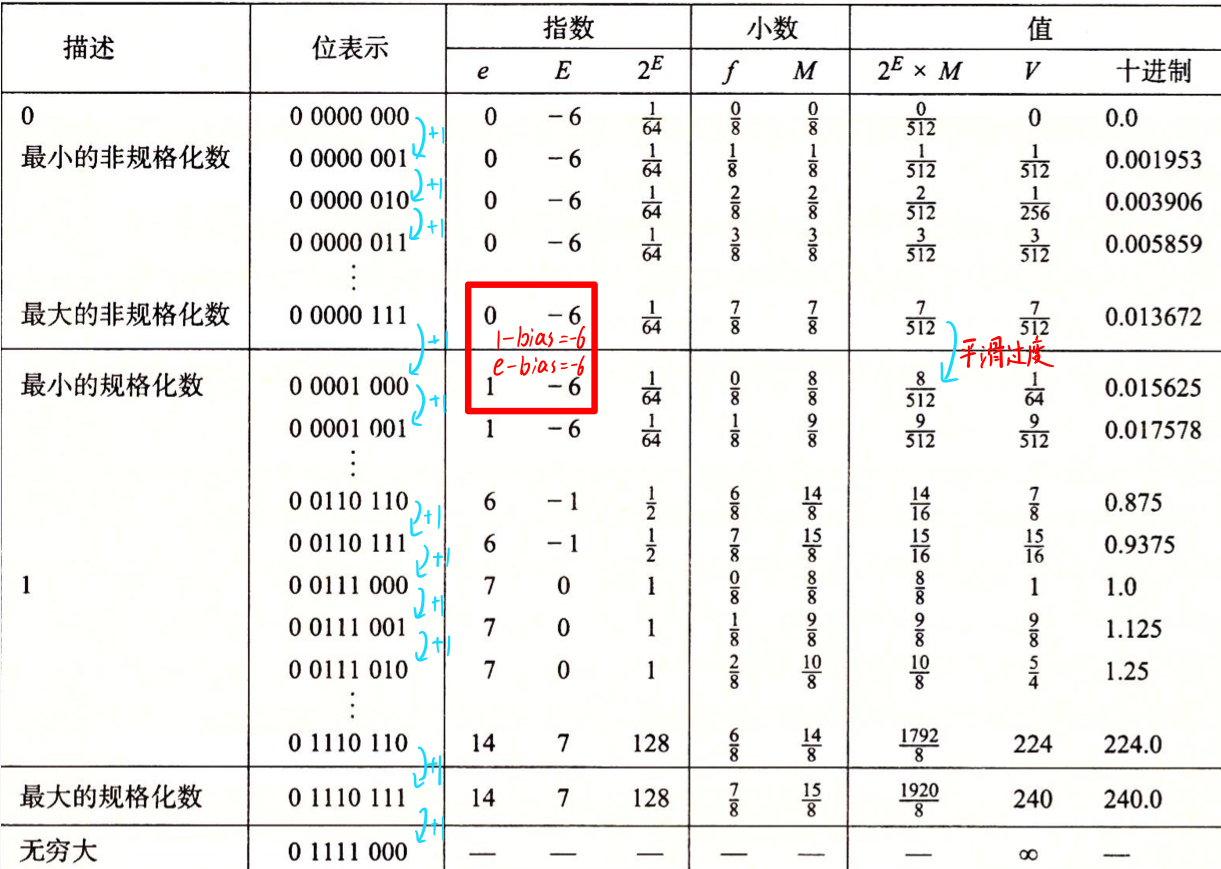
假定的8位浮点格式

可以看见，最大非规格化数 $\frac {7} {512}$ 到最小规格化数 $\frac {8} {512}$ 的平滑转换。这种转换归功于对非规格化数的 E 的定义，其可以弥补非规格化数的尾数没有隐含的开头的 1 。

同时还可以发现，当把上图中的位表达式解释为无符号数时，其就是升序排列的！ 这并非偶然，IEEE 格式如此设计就是为了使浮点数能够使用整数排序函数来进行排序。

规格化数的用途：

提供了表示浮点 0 的方法。因为使用规格化数，mantissa 必须的整数部分一定为 1，所以无法表示 0 。当所有域都为 0 时，表示 +0.0 ；当符号位为 1 ，其他域为 0 时，表示 -0.0 。
表示那些很接近 0 的数

一些运算的结果不能是实数或无穷，就会返回 NaN，比如计算根号下-1 或 ∞ - ∞ ，有时也可以用来表示某些未初始化的数据。

精度

计算机浮点误差主要来源于：一个有限位数的小数并不一定能转换成有限位数的二进制，只有末位是 5 的小数才 有可能 转换成有限位数的二进制，其它的小数都不行。 float 和 double 的尾数部分是有限的，固然不能容纳无限的二进制；即使小数能够转换成有限的二进制，也有可能会超出尾数部分的长度，此时也不能容纳。这样就必须“四舍五入”，将多余的二进制“处理掉”，只保留有效长度的二进制，这就涉及到了精度的问题。也就是说，浮点数不一定能保存真实的小数，很有可能保存的是一个近似值。
对于 float，尾数部分有 23 位，再加上一个隐含的整数 1，一共是 24 位。最后一位可能是精确数字，也可能是近似数字（由四舍五入、向零舍入等不同方式得到）；除此以外，剩余的 23 位都是精确数字。也就是说，整体的精度为 23~24 位。如果转换成十进制， $2^{24}= 16 777 216$ ，一共8位；也就是说，最多有 8 位有效数字，但是能保证的是 7 位，从而得出整体精度为 7~8 位。对于 double，同理可得，二进制形式的精度为 52~53 位，十进制形式的精度为 15~16 位。

比如， $0.5=1×2^{-1}$ ， $0.75 = 1×2^{-1}+1×2^{-2}$ ；而 0.55 与 0.755 就无法用有限的二进制位表示。

过程示范：

将 12345 转为浮点格式：

12345 = $1.1000000111001_2 × 12^{13}$
丢弃尾数开头的 1 ，并在末尾增加 10 个 0 ，来构造尾数字段，得到 10000001110010000000000

注意，小数是在末尾添 0 ，整数是在开头添 0
13 + 127 = 140 ，其二进制为：10001100
符号位为 0
得到 01000110010000001110010000000000

同时可以发现，整形 12345 和浮点 12345 有如下对应关系：

// 整形 00000000000000000011000000111001
// 箭头                    ⬇···········⬇
// 浮点           01000110010000001110010000000000

浮点的尾数部分与整形第一位后的所有位相对应。

待续