问题描述

假设有排成一行的 N 个位置记为 1~N ，N >= 2 。开始时机器人在其中的 start 位置上。规定机器人每次只能向左或向右移动一步，且不能越过边界（即如果机器人来到 1 位置，那么下一步只能往右来到 2 位置；如果机器人来到 N 位置，那么下一步只能往左来到 N-1 位置）。
要求机器人必须走 steps 步，最终能来到 aim 位置的方法有多少种。给定四个参数 start、N、steps、aim ，返回方法数量。

暴力递归

此类题的递归分支设计十分简单，就两个选择——向左或向右，这两种情况都尝试即可，容易得到以下代码：

//暴力递归
//pos-当前位置,step-剩余可走的步数,counts-总方法数
void process(int N, int pos, int aim, int step, int &counts)
{
    if(start <= 0 || start > N)//越界处理
        return;
    if(step == 0)
    {
        if(start == aim)//此路径可行
        {
            counts++;
            return;
        }
        else
            return;
    }
    process(N, start - 1, aim, step - 1, counts);//向左走
    process(N, start + 1, aim, step - 1, counts);//向右走
}

int robotWalk(int N, int start, int aim, int steps)
{
    int counts = 0;
    process(N, start, aim, steps, counts);
    return counts;
}

这个思路可能是最容易想到的，但它并不利于动态规划，因为动态规划的状态转移方程一般是类似于数学归纳法中的递推公式或者数列中的通项公式，如下：

$dp(i, j) = dp(i+x, j+y) + dp(i+m, j+n)$

也就是说，我们最好将递归函数 process 设计为有返回值的函数 ，这样更有利于后续的动态规划分析。修改见下。

暴力递归-改进

int process1(int N, int pos, int aim, int step)
{
    if(start <= 0 || start > N)
        return 0;
    if(step == 0)
    {
        if(pos == aim)
            return 1;
        else
            return 0;
    }
    //在pos位置上尝试向左和向右走,返回这两种路径的方法数总和
    return process1(N, pos - 1, aim, step - 1) + process1(N, pos + 1, aim, step -1);
}

int robotWalk1(int N, int start, int aim, int steps)
{
    return process1(N, start, aim, steps);
}

这样我们就得到了带返回值的 process1 函数。继续观察后发现，在整个递归过程中，N 和 aim 都是不变的，变化的参数只有 aim 和 step 。于是我们可以将 aim 和 step 这两个参数理解为 process1 函数的状态变量，也就是说，当前递归的状态完全由此二参数决定。这所谓的状态变量有什么用呢？有用，来看看下面的例子：

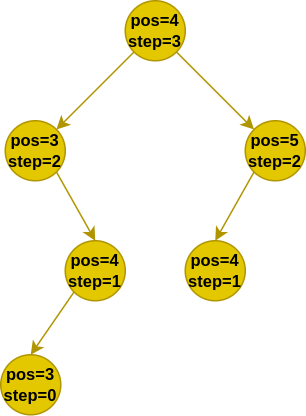
如上图，可以发现在递归过程中会出现状态相同的时候，即出现了两次 pos=4 , step=1 的状态。现在问题是，如果递归时发现之前已经出现过相同的状态，那么还需要继续往下递归吗？不需要。为什么？因为对于计算机而言，你向函数提供与之前相同的参数，那么函数必定返回与之前相同的结果。所以当出现了与之前相同的递归状态时，直接返回先前获取的值即可。因此我们还需要一张表来记录“先前获取的值”以及该值对应的状态，后续如果出现了相同的状态，我们直接查表取值，不再进行后续递归。这种方法被称为 记忆化搜索，也称为自顶向下的动态规划，往往可以大幅删减递归分支（剪枝）。

记忆化搜索

由于此问题的递归函数有 pos 和 step 两个状态变量，所以需要一个二维数组作为二维表来记录值。易知 pos 的范围是 1~N ，所谓表的规格为(N+1)*(steps+1) 。为什么加 1 ？这是个很容易踩进的小坑！一共有 N 个位置，且位置范围为 1~N（从 1 而非 0 开始算），所以数组应该有 (N+1)行，如果错误地将其大小设置为 N ，那最多只能走到 N-1 位置。而剩余步数 step 可以为 0，即范围为 0~steps，所以数组应该有(steps+1)列。

这个坑也会大量出现在后续的动态规划题目中，务必引起注意！

代码如下：

int process2(int N, int pos, int aim, int step, vector<vector<int>> &memo)
{
    if(pos <= 0 || pos > N)
        return 0;
    if(memo[pos][step] != 0)//如果发现之前有过记录,直接返回该值
        return memo[pos][step];
    if(step == 0)
    {
        if(pos == aim)
            return 1;
        else
            return 0;
    }
    int count = process2(N, pos - 1, aim, step - 1, memo) + process2(N, pos + 1, aim, step -1, memo);
    memo[pos][step] = count;//添加记录
    return count;
}

int robotWalk2(int N, int start, int aim, int steps)
{
    vector<vector<int>> memo;//备忘录
    memo.resize(N + 1); ///注意+1！！！
    for(int i = 0; i <= N; i++)
    {
        memo[i].resize(steps + 1);
        for(int k = 0; k <= steps; k++)
        {
            memo[i][k] = 0;
        }
    }
    return process2(N, start, aim, steps, memo);
}

将目光转回到第 14 行的递推关系式：

$count=process2(N,pos-1,aim,step-1,memo)+process2(N,pos+1,aim,step-1,memo)$

count 是当前递归状态下的局部变量，所以可以写成以下形式：

$process2(N,pos,aim,step,memo)=process2(N,pos-1,aim,step-1,memo)+process2(N,pos+1,aim,step-1,memo)$

而递归状态与 N、aim、memo 无关，所以可以继续简化：

$process2(pos,step)=process2(pos-1,step-1)+process2(pos+1,step-1)$

以上表达式就是所谓的“状态转移方程”。

memo表虽然可变，但它只是用来记录各个状态对应的值，并不能算作状态变量。

表位置依赖

我们花了大力气得到的状态转移方程又有何用呢？将该方程体现在表中就会有所发现：

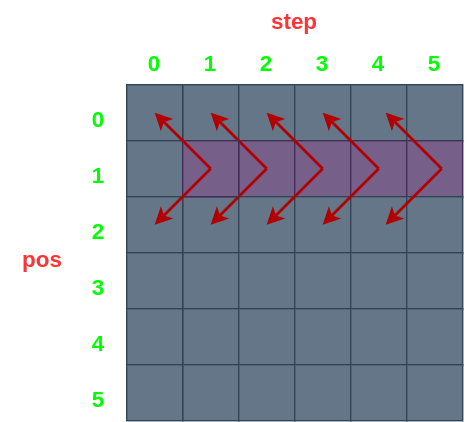
可以直观地看到，每个格子都依赖于左上方和左下方的格子，对于位于边界的格子只需要做一些特殊处理即可。那么我们最终想要的结果应该从哪个格子中获取？当然是 memo(start, steps) 。也就是说，整个问题从递归求解转变为了填表格游戏！当填下 [start,steps] 处的格子时，我们便得到了最终答案！

所以剩下的问题就是如何填表。填表有两种方式：1）先对特殊位置进行初始化，再填写普遍位置；2）直接统一处理，但每次填表时需要先检查基线条件。

方法一：

观察基线条件：pos <= 0 或 pos > N 时返回 0，所以我们先将第 0 行填 0 。
发现每个格子都依赖于左列，所以填表格时必须按列从左往右填，因此我们必须先填第 0 列。

不妨将这一步操作称为特例初始化。有了特例作为启动子，才能完成后续普遍的填表流程。
再观察基线条件：step = 0 且 pos = aim 时返回 1，因此 memo[0][aim] 处须填 1，第 0 列其他行则填 0 。
对于剩下的格子，也可以直接初始化为 0（初始化为其他数也没有影响）。
第一列有了，所以我们按列从左往右依次填写即可，对于边缘格子做特殊处理。

假设 N = 5 ，aim = 5 ，steps = 5 ，start = 3，则表格初始化如下：

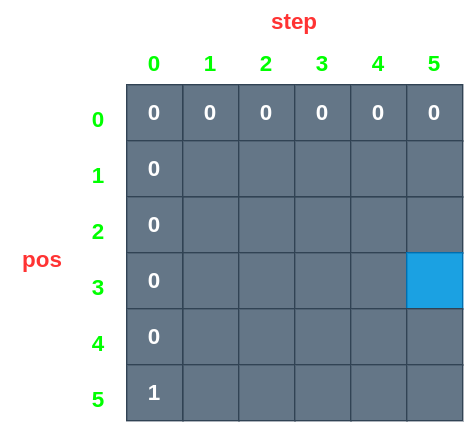
蓝格子则是我们最终想要获取的值。代码如下：

int robotWalk3(int N, int start, int aim, int steps) 
{
    vector<vector<int>> dp;
    //初始化表格
    dp.resize(N + 1);
    for (int i = 0; i <= N; i++)
    {
        dp[i].resize(steps + 1);
        for (int k = 0; k <= steps; k++) 
        {
            dp[i][k] = 0;
        }
    }
    dp[aim][0] = 1;
    
    //从左往右依次填写
    for (int c = 1; c <= steps; c++)//从第1列往右填
    {
        dp[1][c] = dp[2][c - 1];//第1行只依赖第2行左列
        for (int r = 2; r <= N - 1; r++) //从第2行开始依次填写
        {
            dp[r][c] = dp[r - 1][c - 1] + dp[r + 1][c - 1];
        }
        dp[N][c] = dp[N - 1][c - 1];//第N行只依赖第N-1行左列
    }
    return dp[start][steps];
}

方法二：

填表之前必须判断基线条件：

int help(int n, int start, int aim, int step, const vector<vector<int>> &map)
{
    if(start <= 0 || start > n || std::abs(start - aim) > step)
        return 0;
    if(step == 0)
    {
        if(start == aim)
            return 1;
        else
            return 0;
    }
    return map[start][step];
}
int robotWalk(int n, int start, int aim, int step)
{
    vector<vector<int>> map;
    map.resize(n + 1, vector<int>(step + 1, 0));
    map[aim][0] = 1;
    for (int c = 0; c <= step; c++)
    {
        map[1][c] = map[2][c - 1];
        for (int r = 0; r <= n; r++)
            map[r][c] = help(n, r - 1, aim, c - 1, map) + help(n, r + 1, aim, c - 1, map);
    }
    return map[start][step];
}

个人认为第二种方法更加方便。

总结

从暴力递归到动态规划的过程：

先想出暴力递归，且要求通过返回值传递答案。
观察参数哪些可变、哪些不变，可变的即为状态变量。

容易知道，我们最好控制状态变量的个数，否则表维度过高不利于分析。
简单举例判断递归过程中是否存在相同的状态，如果不存在，就没有继续改为动态递归的必要。
改为记忆化搜索（可省略）。
通过递推关系式分析表格的位置依赖，进一步修改为表位置依赖（自底向上）的动态规划。
填表有两种方法：1）特例初始化；2）统一处理。