方法论

之前用二叉树递归解决问题时，总是凭感觉在写递归，状态差时就很容易被绕进去。直到最近学到一套利用树形动态规划解决问题的通用方法，才明白原来思路可以这样清晰，只需要列全可能性，问题就被解决了一大半。

该方法适用于树形动态规划问题，其具体操作如下：

假设以 X 节点为头，假设可以向 X 左树和 X 右树要任何信息
在上一步的假设下，讨论以 X 为头节点的树，得到答案的可能性(最重要)
列出所有可能性后，确定到底需要向左树和右树要什么样的信息
把左树信息和右树信息求全集，就是任何一棵子树都需要返回的信息 S
递归函数都返回 S，每一棵子树都这么要求
写代码，在代码中考虑如何把左树的信息和右树信息整合出整棵树的信息

动态规划：通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法，常常适用于有重叠子问题和最优子结构性质的问题。

我们举几道题目来应用以上方法。

判断是否为满二叉树

满二叉树，即对一棵二叉树中的所有子节点而言，要么没有孩子，要么同时有左右两个孩子。

本题很简单，首先我们确定本节点需要向左右子节点询问什么信息，由上面的满二叉树定义可以得知，如果一棵树是满二叉树，则须满足：

根节点的左右子树都是满二叉树
根节点的左右子节点要么都是空，要么都不为空

注意，第一个要求很容易被忽略！这类要求是解决树形动态规划的关键！它将原问题又分解成类似的子问题，达到各个击破 ，后面的例子也会见到类似的要求。

因此 X 节点需要向其左右子节点索要的信息为：

你（即该子节点）是否为满二叉树
你是否为空

所以就很容易得到如下代码：

//0-null, 1-true, 2-false
int judgeFullTree_in(TreeNode* root)
{
   if(root == nullptr)
       return 0;
   int lc = judgeFullTree_in(root->left);
   int rc = judgeFullTree_in(root->right);
   if(lc == 0 && rc == 0)
       return 1;
   if(lc == 1 && rc == 1)
       return 1;
   if(lc + rc == 1)
       return 2;
   if(lc == 2 || rc == 2)//子树是否都为满二叉树
       return 2;
}

bool judgeFullTree(TreeNode* root)
{
    int ret = judgeFullTree_in(root);
    if(ret == 0 || ret == 1)
        return true;
    else
        return false;
}

判断是否为平衡二叉树

平衡二叉树：树中每个节点的左右两子树高度差都不超过 1 的二叉树。

根据定义，我们得知一棵树如果为平衡二叉树，则树中任意节点的左右子树为平衡二叉树，且左右子树的高度差不大于 1。

所以 X 节点应该向左右子节点索要如下信息：

你自己是否为平衡二叉树（空节点视为平衡二叉树）
你的高度

如果左右子树都为平衡二叉树，则比较两子树高度的差值是否大于 1，然后返回判断结果。

struct info
{
    bool isAVL;
    int height;
    info(bool _isAVL, int _height):isAVL(_isAVL), height(_height){}
};

info process(TreeNode* node)
{
    if(node == nullptr)
        return info(true, 0);
    info left = process(node->left);
    info right = process(node->right);
    if(!left.isAVL || !right.isAVL || abs(left.height - right.height) > 1)
        return info(false, -1); //此时不用再判断高度,可传任意值
    return info(true, std::max(left.height, right.height) + 1);
}

bool judgeAVL(TreeNode* root)
{
    if(root == nullptr)
        return true;
    return process(root).isAVL;
}

判断是否为搜索二叉树

二叉搜索树是指一棵空树或者具有下列性质的二叉树：

若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；

若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；

任意节点的左、右子树也分别为二叉查找树；

由上面的定义我们很快能推断出 X 节点应该向左右子树索要如下信息：

你自己是否为搜索二叉树
你树中的最大值和最小值

第二点需要强调的是，根据定义，对于左子树而言应索要最大值；对于右子树而言应索要最小值。虽然对左子树和右子树的要求不同，但这整个过程是在同一个递归函数中进行的，你无法分别对左子树返回最大值，而对右子树返回最小值，只能求两者的全集，后续整理信息时才可以区别对待。代码如下：

struct info
{
    int flag;//-1=null, 0=false, 1=true
    int max;
    int min;
    info(int _flag):flag(_flag){};
    info(int _flag, int _max, int _min):flag(_flag), max(_max), min(_min){}
};

info progress(TreeNode* node)
{
    if(node == nullptr)
        return info(-1);
    info left = progress(node->left);
    info right = progress(node->right);
    if(left.flag == -1 && right.flag == -1)
        return info(1, node->data, node->data);
    if(left.flag == -1 && right.flag == 1 && right.min > node->data)
        return info(1, right.max, node->data);
    if(left.flag == 1 && right.flag == -1 && left.max < node->data)
        return info(1, node->data, left.min);
    if(left.flag == 1 && right.flag == 1 && left.max < node->data && right.min > node->data)
        return info(1, right.max, left.min);
    return info(0); //其他情况一律为false
}

bool judgeBST(TreeNode* root)
{
    if(root == nullptr)
        return true;
    return progress(root).flag;
}

当 node 为 nullptr 时，此处的处理和之前的几道题有所不同。因为本题中当 node 为 nullptr 时，你不好确定这个空节点的 max 和 min 为多少，所以我们兼用 info 结构体中的 flag 变量来判别节点是否为空（flag = -1 时），然后在上游专门处理节点为空的情况。

二叉树的直径

二叉树的直径是指树中任意两个节点之间最长路径的长度

比如下图的最长路径为 5 ，即路径 6-4-2-5-7-8：

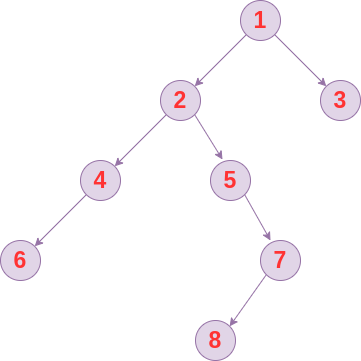
思考后容易知道，最长路径的长度一定为某个节点的左子树高度加上右子树的高度。对每个节点我们求出左子树和右子树的高度和，然后比较整棵树中所有节点的高度和，最大的那个高度和即为二叉树的直径。所以 X 节点需要向左右子树索要以下信息：

你的高度
你的最大高度和

X 节点得到左右子树的高度和后，将本节点的高度和与左子树和右子树的最大高度和进行比较，选出最大的那个高度和，作为本节点的最大高度和，返回返回信息体即可。代码如下：

struct info
{
    int height;
    int maxDis;
    info(int height, int dis):height(height), maxDis(dis){}
};

info findMaxDis_in(TreeNode* nd)
{
    if(nd == nullptr)
    {
        info inf(0, 0);
        return inf;
    }
    info infl = findMaxDis_in(nd->left);
    info infr = findMaxDis_in(nd->right);

    info infc(0, 0);
    infc.maxDis = std::max(std::max(infl.maxDis, infr.maxDis), infl.height + infr.height);
    infc.height = std::max(infl.height, infr.height) + 1; //别忘了本节点还要+1
    return infc;
}

int findMaxDis(TreeNode* root)
{
    info inf = findMaxDis_in(root);
    return std::max(inf.height - 1, inf.maxDis);//根节点没有父节点,需要-1
}

派对的最大快乐值

本题非常漂亮，因此笔者为其单独写了一篇文章，参见派对的最大快乐值。

本题中，X 节点向各个子节点索要的信息为：你参加或者不参加派对时，你所有下属的最大快乐值为多少。

总结

以上问题都可以归结为树形动态规划问题，其特点是可以将整个问题分解相似的子问题，然后由下到上逐个击破。这套方法的代码可能不是最简洁或者最快的，但它为我们提供了固定的模式，能够快速指明解题方向。

参考：左程云算法课程

树形动态规划的解题思路

方法论

判断是否为满二叉树

判断是否为平衡二叉树

判断是否为搜索二叉树

二叉树的直径

最近公共祖先

派对的最大快乐值

总结