拓扑排序的三种方式(附题目)
前言
用大白话说,拓扑排序就是一种对依赖关系的排序,比如编排课表就需要用到拓扑排序:假设你这学期要学习代号为 1,2,3,4,5,6 这六门课程,它们的依赖关系如下:
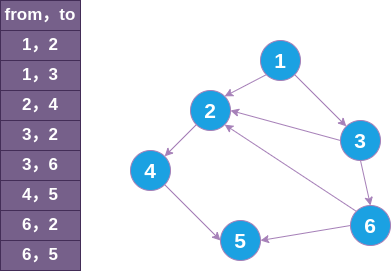
也就是说,如果你想学习 ③ 课程,就必须要先学 ① 课程;如果想学 ② 课程,就必须先学 ①、③、⑥课程。
那么我们就需要对这些课程进行排序以保证每门课的前置课程都学过,这种排序就是拓扑排序。除了编排课程表,拓扑排序还经常用在编译顺序中。
需要注意的是,仅对于有向无环的图才可以使用拓扑排序,否则,① 课程的前置课程为 ②,而 ② 的前置课程为 ① ,那你到底应该先学哪个呢?这就出现了环,是无法进行拓扑排序的。
下面给出三种思路完成拓扑排序。
卡恩算法
卡恩算法的思想为:由于是有向无环图,所以图中一定有至少一个节点的入度为 0(即没有其他节点指向它);删除该节点后,图中一定会产生新的入度为 0 的节点;重复以上过程,依次打印入度为 0 的节点,所得顺序即为拓扑序。算法如下(头文件参见图的适配器):
#include"graph.h"
list<graphNode*> topologySort1(const graph& gra)
{
list<graphNode*> result;
queue<graphNode*> zero_in; //存放入度为0的节点
unordered_map<graphNode*, int> map_in; //存放节点和入度的映射关系
graphNode* tmp;
int counter = 0;
for(auto n : gra.nodes)
map_in.emplace(n.second, n.second->in); //依次映射节点和入度
for(auto n : gra.nodes)
{
if (n.second->in == 0) //初始时刻将入度为0的节点都放入队列
zero_in.push(n.second);
}
while(!zero_in.empty())
{
tmp = zero_in.front();
zero_in.pop();
counter++;
result.push_back(tmp);
for(auto n : tmp->nexts)
{
map_in[n]--; //删去该节点后,其邻节点的入度都需要减1
if(map_in.at(n) == 0)
zero_in.push(n);
}
}
if(counter != gra.nodes.size())
{
std::cout<<"图中存在环,无法进行拓扑排序..."<<std::endl;
exit(-1);
}
return result;
}
其中 counter 记录整个过程中入度曾降到 0 的节点的个数,作用是用来判断图中是否存在环。这是因为,如果图中有环,那么最终 counter 一定小于图中的节点总数。
深度优先
仔细一想,似乎能够发现:深度越大的节点依赖的前置节点越多。所以在深度遍历时,我们将深度大的节点先入栈,深度浅的节点后入栈,最后依次出栈时,先出栈的节点依赖程度最小,后出栈的节点依赖程度增大,这看起来也像是拓扑序。抱着试一试的形态,我们写出下面的代码:
void DFS(graphNode* node, unordered_set<graphNode*>& visited
,unordered_set<graphNode*> visitedInPath, stack<graphNode*>& stk)
{
if(visitedInPath.find(node) != visitedInPath.end())//不可与下面的if交换位置
{
std::cout<<"图中存在环,无法进行拓扑排序..."<<std::endl;
exit(-1);
}
if(visited.find(node) != visited.end())
return;
visited.emplace(node);
visitedInPath.emplace(node);
for(auto n : node->nexts)
DFS(n, visited, visitedInPath, stk);
stk.push(node);
}
// 拓扑排序
list<graphNode*> topologySort2(const graph& gra)
{
stack<graphNode*> stk;
list<graphNode*> ret;
std::unordered_set<graphNode*> visitedInPath;
unordered_set<graphNode*> visited;
for (auto it : g.nodes)
DFS(it.second, visited, visitedInPath, stk);
while(!stk.empty())
{
ret.push_back(stk.top());
stk.pop();
}
return ret;
}
visitedInPath 用来判断当前路径中是否有环,注意此参数不能引用!visitedInPath 对每条路径都是独立的,如果加上引用,将变为全局表。
可见该代码和图的深度优先遍历代码非常相似,只是多了环的判断和入栈过程。试验如下:
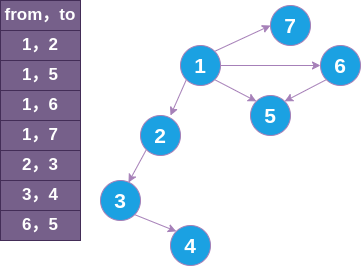
int main()
{
vector<vector<int>> nodes = {{0,1,2},
{0,1,5},
{0,1,6},
{0,1,7},
{0,2,3},
{0,3,4},
{0,6,5}};
graph gra = graphAdaptor(nodes);
auto ret1 = topologySort1(gra);
auto ret2 = topologySort2(gra);
for(auto n : ret1)
std::cout << n->value << ", ";
std::cout << std::endl;
for(auto n : ret2)
std::cout << n->value << ", ";
std::cout << std::endl;
}
1, 2, 6, 5, 7, 3, 4,
1, 2, 6, 7, 3, 5, 4,
以上两种顺序均正确。
高度比较
X 节点的最大高度是指,以 X 为起点进行深度优先遍历,所得最长的那条路径的长度。比如下图中 ① 节点的最大高度为 4,即路径[1-2-3-4]。

所以容易得出结论:如果图中存在 X、Y 两个节点,且 X 的最大高度 > Y 的最大高度,则拓扑序一定有 X <= Y
为什么是小于等于呢?因为 X 的最大高度 > Y 的最大高度分为两种情况:
- Y 包含在 X 的路径中
- Y 不包含在 X 的路径中
如果是第一种情况,则拓扑序 X < Y( X 一定排在 Y 之前);
如果是第二种情况,则拓扑序 X=Y(两者顺序不定,取决于图的组织方式)。
所以这里关键在于求节点的最大高度。代码见题目1。
题目1-拓扑排序
题目描述以及代码提交请点击此处。
本题我们使用之前的 高度比较方法 来解决。由于题目中给的 DirectedGraphNode 结构没有高度描述,所以需要自己建立一个包装类,即下面代码中 wrap 。下面代码还使用了一张缓存表来记录各个节点的最大高度,也就是说,如果之前已经得到了 X 节点的最大高度,后续遍历到 X 节点时就直接从缓存表中查询即可,不然如果图规模较大,每次重复遇到一个节点时都深度遍历一次,那么耗时将相当可观。这种建立缓存的思想属于动态规划,以后我们会大量遇到此类问题。
struct DirectedGraphNode
{
int label;
vector<DirectedGraphNode *> neighbors;
DirectedGraphNode(int x) : label(x) {};
};
struct wrap
{
DirectedGraphNode* node;
int depth;
wrap(DirectedGraphNode* _node, int _depth):node(_node), depth(_depth){}
};
int process(DirectedGraphNode* node, unordered_map<DirectedGraphNode*, wrap*> &map)
{
if(map.find(node) != map.end()) //之前已经获取,直接查询
return map[node]->depth;
if(node->neighbors.empty())
return 1;
int maxDepth = 0;
int depth;
for(auto n : node->neighbors)//获取子树中最大的高度
{
depth = process(n, map);
wrap* w = new wrap(n, depth);
map.emplace(n, w);
maxDepth = maxDepth > depth ? maxDepth : depth;
}
return maxDepth + 1; //别忘了加上本节点自己
}
vector<DirectedGraphNode*> topSort(vector<DirectedGraphNode*> graph)
{
unordered_map<DirectedGraphNode*, wrap*> map;
int depth;
for(auto n : graph)
{
depth = process(n, map);
wrap* w = new wrap(n, depth);
map.emplace(n, w);
}
vector<pair<DirectedGraphNode*, wrap*>> vec;
for(auto n : map)
vec.push_back(n);
std::sort(vec.begin(), vec.end()
, [](pair<DirectedGraphNode*, wrap*> a, pair<DirectedGraphNode*, wrap*> b)
{return a.second->depth > b.second->depth;});//这里使用lambda函数作为比较器进行排序
vector<DirectedGraphNode*> ret;
for(auto n : vec)
ret.push_back(n.first);
return ret;
}
第 19-30 是核心代码,用来递归寻找图节点的最大高度。
另外,本题也可以使用 深度优先方法 破解,直接给出代码:
void DFS(graphNode* node, unordered_set<graphNode*>& visited
,unordered_set<graphNode*> visitedInPath, stack<graphNode*>& stk)
{
if(visitedInPath.find(node) != visitedInPath.end())
exit(-1);
if(visited.find(node) != visited.end())
return;
visited.emplace(node);
visitedInPath.emplace(node);
for(auto n : node->nexts)
DFS(n, visited, visitedInPath, stk);
stk.push(node);
}
vector<DirectedGraphNode*> topSort(vector<DirectedGraphNode*> graph)
{
stack<graphNode*> stk;
vector<graphNode*> ret;
std::unordered_set<graphNode*> visitedInPath;
unordered_set<graphNode*> visited;
for (auto it : g.nodes)
DFS(it.second, visited, visitedInPath, stk);
while(!stk.empty())
{
ret.push_back(stk.top());
stk.pop();
}
return ret;
}
题目2-课程表
题目描述以及代码提交请点击此处。
此题的本质就是判断图中是否有环,方法已在前文讲述,不再赘述。
